Quantum bits don't byte
An introduction to the world of quantum computing
by Dr. Tomás Silveira Salles
18 minute read
Quantum computing is fascinating, counter-intuitive, more than 30 years old and yet still futuristic, among many other adjectives. What it is not, is magic.
The mountains of quantum computing magazine articles aimed at the general public are covered in sensational headlines that I find misleading in the worst possible way: They lead people to think "this stuff is for the scientists of the world to understand, and for mere mortals like me to hopefully one day use". What's even more annoying is that quantum computing doesn't need any controversial, provocative statements to embellish it. It is amazing all by itself, bare. Unfortunately, it is indeed not for everyone, but interested readers can definitely go further than the popular channels seem to believe, and get a good taste of what it's really all about.
If you've never heard of quantum computing, this is probably not the best starting point. On the other hand, I still haven't found a good starting point anywhere else, so you might as well give this article a try.
The very basic, in a pistachio shell
To understand quantum computers we need to separate the concept “computer” from the machines we use every day
In order to even be able to think about a new type of computer, we first need to separate the general concept of "computer", from the actual machines we use every day, and the same goes for the concept of "bit". So from now on, we refer to ordinary computers as classical computers and ordinary bits as classical bits and use more abstract definitions for the two original terms:
A bit is just an entity on which you can apply an operation called reading (or measuring), and the output of the reading operation is binary, i.e. has exactly two possible values, usually 0 and 1.
A logic gate is an operator that you can apply to one or more bits in order to modify and combine their internal properties. What internal properties are available, depends on the kind of bit you are using.
A computer is a machine that uses bits and logic gates to perform algorithms. By this I mean that (once prepared for a specific algorithm) a computer receives a binary string as input and uses it to somehow prepare an array of bits. Then these bits pass through a series of logic gates which manipulate and combine them. In the end, the bits are read, so as to produce a new binary string, which the computer returns as the output of the algorithm.
Now imagine if we used, for example, the nucleus of an atom as a bit, and measured its spin's direction when "reading" it (thus obtaining either "spin up", or "spin down" as output). This would be an example of what is called a qubit (or "Qbit", "QBit", "Qubit", "q-bit", "qbit" etc). The "bit" bit of "qubit" is short for "binary digit", which refers to the nature of the measurement's output, while the "qu" bit of "qubit" is short for "quantum", which refers to the fact that the concept is based on the behaviour of certain quantum systems (such as the nucleus of an atom). A computer that uses qubits as its bits is called a quantum computer.
More than just new hardware
The mathematics behind it is completely different from classical computing and allows for new approaches to solve our problems
Each time new materials and technologies make classical computers faster and more powerful, the mathematics to design and control them becomes harder, but the difference is superficial. The mathematical foundation that drives the computer algorithms of today is still basically the theory developed by Alan Turing in the 30's and 40's.
Quantum computing, however, changes the game completely. The concept in itself says nothing about the speed of the computations, or the size of the machines. In fact, the experimental ones we have today are ginormous monsters that probably dream of becoming as fast as your smart-toaster. But the mathematics behind it is completely different, and allows us to try new approaches to solve our problems, instead of just accelerating the old ones.
Now, to business!
(Not so) classical computers
The computers we use today have spoiled us by allowing us to think of a bit in the machine and in an algorithm as the same thing. In other words, the physical implementation and the theoretical concept work so similarly that separating the two is rarely important. The same goes for the state of a bit (i.e. the values of its internal properties) and the output of reading a bit. We just think of a bit as something that is 0 or 1, and reading it just means looking at it to find out which one. Qubits and their strangeness force us to look at all of this from a more mature perspective.
In the processor inside your laptop, bits are implemented as voltage differences applied to electrical wires. We can achieve a high voltage on a wire by connecting one of its ends to a power supply, and a low voltage by disconnecting it. However, the process of connecting and disconnecting is not instantaneous, and the voltage difference on the wire doesn't just jump between minimum and maximum. As the wire is connected, the voltage gradually rises from a low value, through a continuous range, up to a high value. The low value is not always the same, but there is a range of low values which we accept as representing 0. The high value is also not always the same, but there is a range of high values which we accept as representing 1. Between the low range and the high range we have a grey area in which measurements would not be accurate enough.
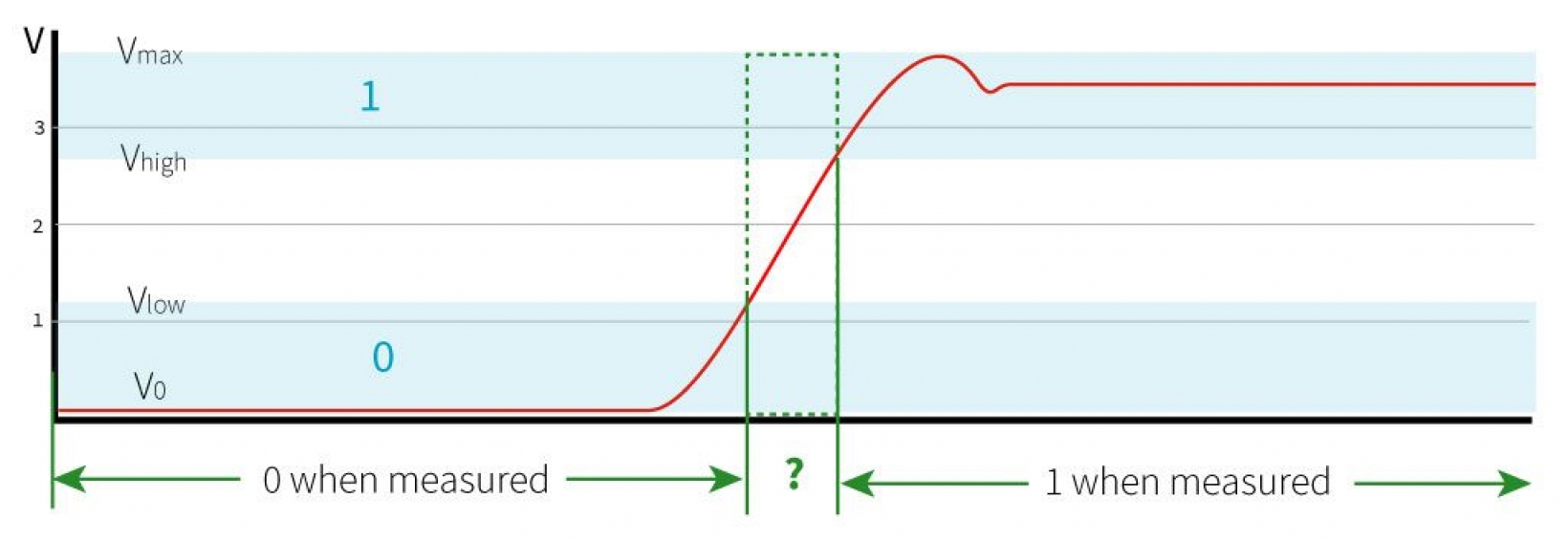
Wibit values charted as voltage over time
Now, we could invent a type of bit that more closely resembles the behaviour of these wires and call it wibit (for "wire bit"). A wibit would have a state which is a number in the interval . To "read" or "measure" a wibit we would choose two more special values and such that , and we would map all values in to 0, all values in to 1, and all values in would be mapped randomly, using a distribution that makes higher values more likely to output a 1 and lower values more likely to output a 0.
The complications go even further, though. There is also the fact that if you place two wires very close to each other on a chip, they start affecting each other. A current through one wire generates an electromagnetic field that can generate a current on the other wire. To code this into our wibits, we'd have to add the possibility of two or more wibits being somehow interconnected. Maybe there's a better word for that... something that says they're all tied up together as if by an intricate mesh of strings and it's difficult to separate one from the other... hm, beats me.
Unfortunately, we never found any usefulness in wibits and have instead always taken their complexity to be our enemy. That's why endless resources have been invested into making the electrical wires behave less like wibits and more like classical bits. We carefully control the spacing between wires to reduce noise, and carefully time the moments when the voltage is "read" to make sure it's not in that ugly grey area, among so many other obstacles. But with qubits, it actually turns out that their weirdness can be used to our advantage, so we embraced it.
Neither 0, nor 1, nor both at the same time
It's hard to find an introduction to quantum computing article without some variation of the sentence "unlike a classical bit, which can only be 0 or 1, a qubit can be 0, or 1, or both at the same time!". See, even this one has it. Here is where this confusing idea comes from:
A qubit sometimes has a property called state (when exactly? See below). When it does, its state is simply... a point on the unit sphere of a 2-dimensional complex Hilbert space. Fair enough, both the space and the sphere are impossible to draw or even visualise. Don't be deceived by the word "sphere": this sphere looks nothing like a beach ball. So yes, we do need to simplify the concept for non-mathematicians, but there's no reason to go as far as "0 and 1 at the same time". For a less radical simplification, let's just replace the word "complex" with "real" above. The unit sphere of a 2-dimensional real Hilbert space is just an ordinary circle, so we can make an analogy between our simplified qubit and a compass, comparing the state of the qubit to the direction in which the needle is pointing.

We choose two special states, say East and South (they just have to be 90 degrees apart) that will be mapped to 0 and 1 by measurements. The measurement operation is random, but the state of the qubit determines what the probability of measuring 0 and the probability of measuring 1 are. In other words, when we measure the qubit we basically flip a coin, but it's a coin that might fall more often on one side than on the other. The position of the needle determines which side is preferred, and how much. If the needle is pointing East, the next measurement will definitely output a 0. If it points almost to the east but not quite (as in the picture above), it will probably output a 0, but might output a 1. If it points exactly Southeast, the output will be 0 half of the time and 1 half of the time.
Note that it doesn't make sense to say that "the state of the qubit is 0", or "the state of the qubit is 1". The state is a needle direction, not a binary digit. Moreover, since states are vectors (with 2 coordinates, in our simplified analogy), they can be combined using vector sums, so that every possible needle direction can be described using only the two special directions/vectors East and South. For example, we can write:
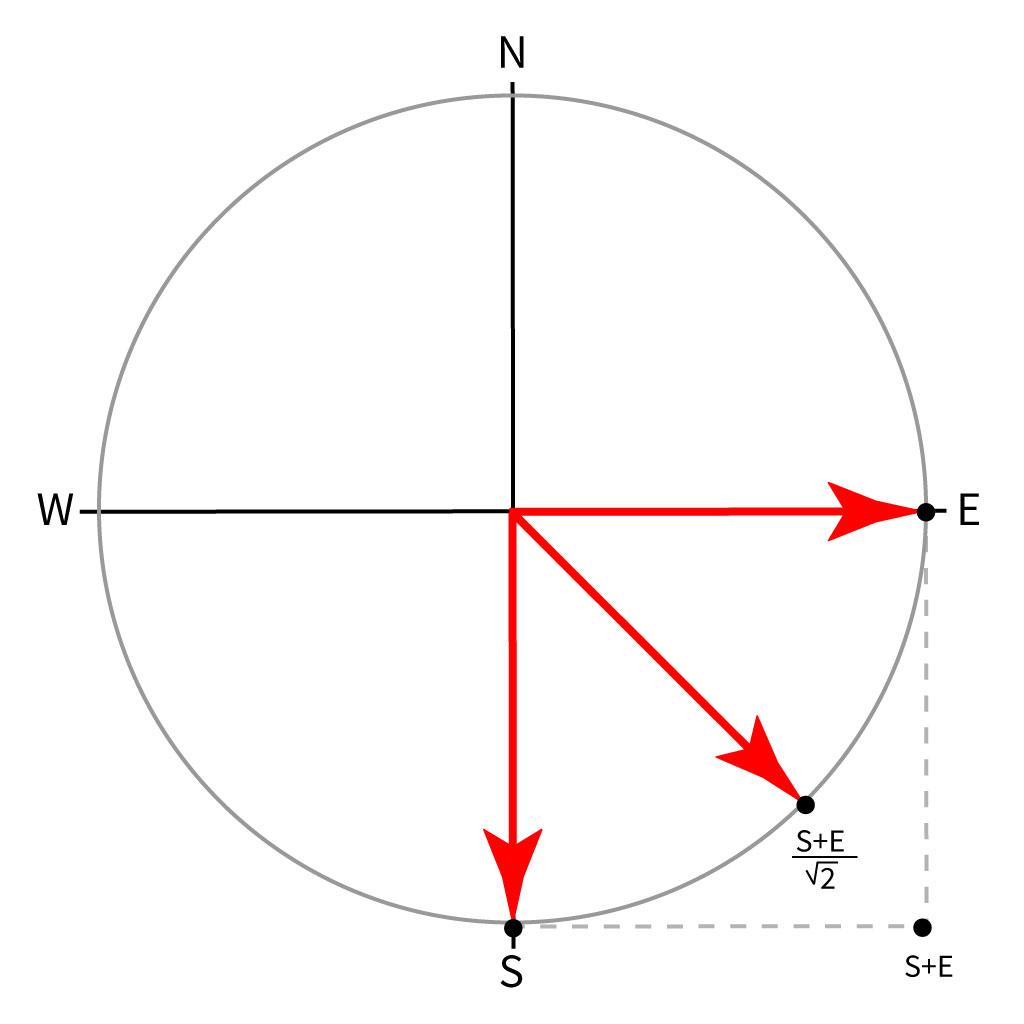
Feel free to start a forum thread to discuss whether Southeast is "South and East at the same time" or "neither South nor East". That discussion is not so much about computer science as it is about language. The important thing is to understand that the state of a qubit is a point on a circle (just not a circle you can draw).
Note: If you've read about quantum computing before, you will have noticed I didn't mention the term superposition. In this context, superposition is just another word for "combination", or more precisely "linear combination". For example, in the equation above we have described Northwest as a linear combination (or superposition) of East and South. This word is probably one of the many sources of confusion when people read about quantum physics. The word "measurement" (when talking about nuclear spin or quantum states in general) is even worse. One should always be cautious when it comes to physics terminology and try to distinguish between the meaning a word has as a physical concept, and its meaning in everyday language.
All tied up together as if by an intricate mesh of strings and difficult to separate from each other
So the state of a qubit is a lot more than just one "bit" of information. You need 4 real numbers , , , and (together representing 2 complex numbers) to describe it. These numbers have all the freedom in the world as long as they satisfy:
Is that why quantum computers are so powerful? No. Sorry to disappoint. First of all you have the problem that the measurement operation still only outputs 0 or 1, so we loose a ton of information there. Second, even if we could somehow obtain the full state of a qubit (which we cannot), 4 real numbers per qubit is really not that much. We've been approximating real numbers using 64 classical bits for a long time and it's usually more than enough for our needs. Moreover, the normalisation condition above implies that we only need to know the value of 3 of the 4 numbers plus the sign of the last one, so we would only need classical bits to encode each qubit. This might be a largish number, but it is a constant, and would therefore make the number of classical bits needed to simulate a quantum computer linear on the number of qubits used. Not enough to turn the world upside down.
How about the fact that the measurement operation is random, whereas reading a classical bit is not. Is this it? Also not. Simulating randomness is not that hard using classical computers. Again, it's not true randomness, but it's close enough for our needs.
The real deal with quantum computers is entanglement.
Remember how I said qubits don't always have states? Well, thank Zarquon for that! If they did, quantum computers would have long been discarded as expensive, slower versions of classical ones. When you build a quantum computer, and you isolate the qubits in the register from the rest of the world, the collection of qubits in the register has a state. Always. But subcollections (including individual qubits) only have states when they are unentangled from the rest. In case you're waiting for me to define what entanglement means, you just missed it. The definition is that a collection of qubits is entangled if no subcollection has a state of its own. In practice this means that measuring the qubits one after the other is not a sequence of independent operations. The output of each measurement has an influence on the output of all the remaining ones.
Why is this so interesting? Because the state of an entangled collection of qubits has far more degrees of freedom than the state of an unentangled collection of the same size.
The number of parameters needed to describe the state of an entangled collection of qubits is not proportional to the size of the collection, but rather to the number of possible outputs of a measurement.
For a single qubit, the possible outputs are 0 and 1, so you need 2 complex numbers to describe it (remember the 2-dimensional complex Hilbert space?). For 3 qubits, the possible outputs are 000, 001, 010, 011, 100, 101, 110 and 111, so you need 8 complex numbers to describe it. For qubits you need complex numbers to describe their state.
In contrast, when a collection of qubits is fully unentangled (that is, each qubit has its own state), we can use these individual states to describe the state of the collection as a combination of them, so we only need complex numbers in total. Even for a small value like , the difference is already huge between and .
But the additional freedom doesn't come just from the number of parameters available. Entanglement can even provide new states when (in which case ): Suppose you have 2 qubits and and they are unentangled, that is, each one has its own state. Qubit has probability of measuring a 0, and of measuring a 1. Similarly we define and . What is the probability of each possible output for the pair? Easy:
Notice that if , then at least one of and must be 0 as well, no matter how you choose the states for and .
If, however, and are entangled, the state of the pair is described by 4 independent complex numbers (except for normalisation), one for each possible output, and can easily be set such that:
In other words, we can entangle and such that for each of them the output of a measurement has equal chances of being a 0 as of being a 1, but if we measure both, we are guaranteed to obtain two distinct values. This demonstrates the power of entanglement.
Computing no values of a function
Another common oversimplification is usually stated along the lines of: "Suppose you want to compute the values of a function . With a classical computer, you would have no choice but to compute each value separately, but a quantum computer can calculate all values at once!". This one is tougher to explain, but I'll do my best.
It originates from a common preparation routine used in quantum computing algorithms, which we'll call the "all values" trick. Without going into technical details, this is how the trick works: Say your function takes as input 3 binary digits and outputs 2 binary digits. The first thing you'll need is a gate that corresponds to the action of but which you can apply to qubits to modify their states (and it might be very difficult to build such a gate, but let's assume you've done it). To prepare your computer, you'll use 5 qubits in the register: 3 representing the function's input digits, and 2 representing its output digits. First, you apply so-called Hadamard gates to the 3 input qubits, which has the effect of making every possible measurement equally likely for them (in the compass analogy: all 3 needles are directed towards Southeast). Then, you apply the gate you built to replace . This will entangle the 3 input qubits with the 2 output ones. Done.
The result is 5 entangled qubits with the following property: If you measure them all and get the binary sequence as the result, you have the guarantee that .
To be clear, it does not matter in which order the qubits are measured. You can even start by measuring the output qubits (and obtain ), and then measure the input qubits (and obtain ), and you still have the guarantee that .
What this trick does is it encodes the entire function into the entanglement of the qubits, and by "entire function" I mean the complete mapping that it represents, i.e. the collection of pairs of input values and corresponding output values.
It shouldn't be surprising that that's possible. After all, we know that the state of the 5 qubits is composed of several real numbers, and even a single real number would be enough to store the "entire function". Remember that real numbers can have any number of digits in their decimal representation (even infinitely many), and we can use these sequences of digits to code information, just like we use binary sequences to code files in our hard-drives.
It is impressive how fast all that information is encoded, by passing the qubits through a single gate. Unfortunately, this gate usually only exists in theory, and is replaced in practice by a long sequence of smaller, simpler gates that we know how to build, so the number of operations applied to the qubits ends up depending on the complexity of after all.
Did we compute every value of when we encoded it into the entanglement of the qubits? Or did we compute no value of at all at that point, and then computed a single value when we took the measurement? That's another question for a forum thread. While the "computed all values" point of view is not technically wrong, it is very misleading. It makes it seem like the point of this trick was to actually compute values of , and that's a very naïve interpretation.
Computing values of a function with this approach would be absolutely pointless because it could easily be simulated using a classical computer and with much less effort: To simulate measuring the first 3 qubits, just randomly generate a binary sequence . Then, to simulate measuring the 2 remaining qubits, just compute .
The "all values" trick is only useful if it's not directly followed by a measurement. At least not a measurement of all qubits. I will try to explain this through an example below.
Asking the right questions
Entanglement is what makes quantum computers truly powerful. But the best screw driver is still a terrible hammer
The famous algorithm written by Peter Shor in the 90's (that uses quantum computing to break RSA encryption) is one of the best examples of how and when to use a quantum computer.
At the core of the problem we have a function which is just modular exponentiation, that is: We have a fixed number (a chunk of a secret message, encoded and encrypted) and a fixed number (the public RSA key) and is defined by
The algorithm starts with the "all values" trick, but does not perform a full measurement yet. A measurement would only give us some value of , and we could easily do that with a classical computer. Instead, the algorithm cleverly further manipulates the state of the qubits (thus manipulating the probability of each possible measurement output).
The goal in the end is to find out the period of , that is, the smallest positive number such that for every . Using the period one can decrypt the secret message even without factoring the public key. (If you want to know how, check out our article on the basics of RSA encryption.)
After applying the "all values" trick, we measure only the qubits that correspond to the output of the function and obtain some number that we actually don't care about. Now, remember that because of the way the qubits are entangled, if we measured the remaining qubits (but we won't just yet), we would necessarily get a number such that .
How many such are there? Well, we can easily count how many possible measurements of the input qubits exist without this entanglement restriction, which is 2 to the power of the number of input qubits we use. Let's call this value (for input). Since every -th input satisfies , it follows that there are possible measurements now that the qubits are entangled. In other words, in the state of the remaining qubits, there are exactly parameters that are different of 0.
By manipulating the qubits further (using other gates), the algorithm gets to a point where the new values of the parameters are combinations of the old values, and the 's with the highest probability of being measured are the ones very close to multiples of . That's when we finally measure the input qubits.
We're nowhere near being finished -- there's still a lot of complicated mathematics needed to extract the period from the result of the measurement -- but the quantum computer has done its job. From this point we can continue the calculations using a classical computer.
Like I said, it's not for everyone. But there's no need to scare people away with this facade of mystery bordering on fantasy. Quantum computing is scary enough on its own.
 DE
DE

